Partida Rol por web

Let ABC be a triangle with incenter I such that AB = 20 and AC = 19. Point P != A lies on line AB and point Q != A lies on line AC. Suppose that IA = IP = IQ and that line PQ passes through the midpoint of side BC. Suppose that BC = m/n for relatively prime positive integers m and n. Compute 100m + n.

Veamos si me entero:

Dado un triángulo ABC con centro desconocido I, tal que AB=20, AC=19, el punto P, distinto de A (que no de B) está en el segmento AB y el punto Q, distinto de A (que no de C) está en el segmento AC. Suponiendo que IA=IP=IQ y que la línea PQ pasa a través del punto central de la línea BC.

El resto de momento lo dejo. Bien, reflexionando solo veo un modo de que el segmento PQ pase por el punto medio del lado BC, y es que P=B y Q=C.

¿Estoy en lo cierto?

Con incentro I, lo de desconocido te lo has inventado. :P

La traducción es correcta. La reflexión no lo sé. No me he puesto a mirar este aún.

Vale, analizando el problema asumo que "I centro" se refiere a un punto en el interior del triángulo, no a su centro.

En cualquier caso, como dije la única opción para que P y Q estén en los segmentos AB y AC y la línea que los une pase por el punto medio de BC, es que P sea B y Q sea C. Si P y Q estuvieran en la recta donde se incluye el segmento AB y AC, entonces sí habría infinitas soluciones.

Eso implica que podemos establecer IA=IB=IC, es decir, I es equidistante de los tres vértices.

Como te decía, según el enunciado I es el incentro del triángulo. Es decir, el punto donde se cortan las bisectrices de los ángulos del triángulo. Esto no es equivalente al centro del triángulo, ni tiene por qué ser equidistante a los vértices salvo en casos concretos, como el del triángulo equilátero.

En un rato echo un ojo a lo que comentas, a ver si tenemos ya otro problema resuelto.

No estoy seguro de que lo que dices pueda ser cierto.

Si I es equidistante de los tres vértices, I sería el centro de una circunferencia donde están los tres vértices, luego sería el circuncentro. Un punto puede ser incentro y circuncentro, pero creo que sólo en triángulos equiláteros (no lo he comprobado, hablo de cabeza), y este no lo es porque sabemos que un lado mide 20 y otro 19.

No veo por qué P=B y Q=C. Nótese que P está en la línea AB, pero no tiene por qué estar en el lado. Es decir, puede estar fuera del triángulo.

P está en el segmento AB, sin poder ser A. Q está en el segmento AC sin poder ser A. Dicen que el segmento que los une, PQ, tiene que pasar por el centro de BC.

Ahora dibuja en un papel un triángulo cualquiera. Vete tomando puntos de un lado y otro y uniéndolos, y dime cuándo el segmento que los une pasa por el centro del otro lado. Solo ocurre si dicho segnebto es FL tercer lado del triángulo, es decir, si P=B y Q=C.

P está en el segmento AB, sin poder ser A. Q está en el segmento AC sin poder ser A. Dicen que el segmento que los une, PQ, tiene que pasar por el centro de BC.

Ahora dibuja en un papel un triángulo cualquiera. Vete tomando puntos de un lado y otro y uniéndolos, y dime cuándo el segmento que los une pasa por el centro del otro lado. Solo ocurre si dicho segnebto es FL tercer lado del triángulo, es decir, si P=B y Q=C.

Es que no es tomando puntos de un lado y otro. Es tomando puntos de las líneas de los lados. Puedes tomarlos fuera del triángulo.

Por ejemplo:

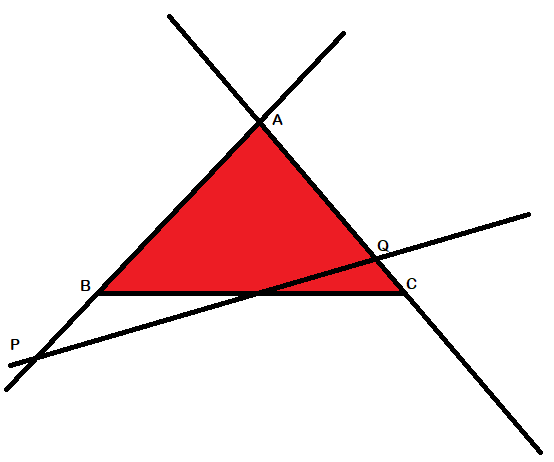
¿Ves? Por eso lo de las traducciones. Si los puntos pueden estar fuera d triángulo, entonces sí es más complicado.